Het hexadecimale talstelsel
Lange reeksen aan enen en nullen typen is onhandig en gemakkelijk om fouten mee te maken. Een efficiëntere methode is het hexadecimale talstelsel (tellen met machten van 16). Één hexadecimaal getal staat voor een heel getal tussen 0 en 15. Dus 4 cijfers in binair kunnen vertaald worden in één cijfer in hexadecimaal en één byte is gelijk aan twee hexadecimale cijfers. Één hexadecimaal getal is veel makkelijker te typen voor mensen en omdat 16 deelbaar is door 2 is het makkelijk om te zetten in binaire getallen.
| Acht bits in binair... | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | ||||
| 128-plek | 64-plek | 32-plek | 16-plek | 8-plek | 4-plek | 2-plek | 1-plek | ||||
| ...is twee cijfers in hexadecimaal 16. | |||||||||||
| 161 | 160 | ||||||||||
| zestien-plek | een-plek | ||||||||||
| Bijvoorbeeld: 12110 = 011110012 = 7916 | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 7 | 9 | ||||||
| 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|
| A | B | C | D | E | F |
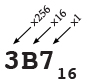
Dit staat voor 3 \times 256 + 11\times 16 +7\times 1 of 951.
-
 Bekijk dit Snap!-programma met een hexadecimale, decimale en binaire teller . De bovenste
rij telt binair, de middelste in decimaal en de onderste in hexadecimaal. Beschrijf het gedrag van
de hexadecimale teller.
Bekijk dit Snap!-programma met een hexadecimale, decimale en binaire teller . De bovenste
rij telt binair, de middelste in decimaal en de onderste in hexadecimaal. Beschrijf het gedrag van
de hexadecimale teller.
Hexadecimale Notatie Lezen
Het hexadecimale talstelsel gebruikt machten van zestien in plaats van machten van twee of tien. Plekken in hexadecimaal staan voor de plek van de eenheden (160 = 1), de plek van de zestientallen (161 = 16), de plek van de tweehonderdzesenvijftigtallen (162 = 256), de plek van de vier duizend zesennegentigtallen (163 = 4096), etc. Dus, bijvoorbeeld:
3B16 = 3 × 161 + 11 × 160 = 48 + 11 = 5910
Om te vertalen van hexadecimaal naar decimaal, schrijf je eerst de cijfers op papier. Dan schrijf je de waardes van de hexadecimale plekken op: begin rechts met 1, dan 16, dan 256 etc. Iedere nieuwe plek zal 16 keer zoveel waard zijn als de plek rechts ervan.
| 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|
| A | B | C | D | E | F |
| 7 | B | 3 |
|---|---|---|
| 256 | 16 | 1 |
 |
||
Dus, 7B316 = (7 × 256) + (11 × 16) + (3 × 1) = 1792 + 176 + 3 = 197110.
- Vertaal deze hexadecimale getallen naar decimale notatie:
- AF16
- 5D16
- 1816
- 3E816
Een getal zoals 11 betekent elf in gebruikelijke, decimale notatie maar het betekent drie als het een binair getal is of zeventien in hexadecimale notatie. De enige manier waarop je weet dat "18" hierboven niet achttien betekent is door de kleine "16" rechtsonder die zegt dat het hexadecimaal is.
= (15 × 161 + 15 × 160)10
= (15 × 16 + 15 × 1)10
= 25510
Hexadecimaal Schrijven
Om te vertalen van decimaal naar hexadecimaal schrijf je eerst de waardes van de hexadecimale plekken op door met zestien te vermenigvuldigen met de waarde rechts ervan tot je een waarde krijgt die groter is dan je getal. Als voorbeeld gaan we 299 omschrijven naar hexadecimal, hiervoor schrijven we de machten van zestien op tot 4096. Je krijgt zo de tabel hieronder.
 |
|||
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
Bedenk dan "Mijn getal is kleiner dan 4096, dus ik hou die plek leeg. Maar ik kan één keer 256 aftrekken van 299, dus ik schrijf daar een 1. Dan is er 43 over, want 299-256=43. Nu kan ik twee keer 16 aftrekken en dan is er 11 over. 11 is B in hexadecimaal"
| 0 |
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 1 | 2 | B |
Lees nu het nummer af: 12B16 = 29910.
- Vertaal deze decimale getallen naar hexadecimaal.
- 59
- 144
- 229
- 316
Merk op dat de algoritmes voor het vertalen van binair naar decimaal hetzelfde is als het algoritme voor het vertalen van hexadecimaal naar decimaal. Deze algortimes kunnen gebruikt worden om elk talstelsel te vertalen.
-
 Je krijgt problemen met het weergeven van talstelsels boven de 36. Wat is het probleem en bedenk een
oplossing?
Je krijgt problemen met het weergeven van talstelsels boven de 36. Wat is het probleem en bedenk een
oplossing? - Vertaal 29910 naar het talstelsel voor 7.