Binaire representatie
We hebben gezien hoe het aantal bits dat gebruikt wordt om een heel getal weer te geven, bepaalt hoe groot het getal kan zijn. Nu gaan we kijken hoe een heel getal precies weergegeven wordt met bits.
In het decimale talstelsel,zijn er 10 cijfers (0-9) en iedere plek is tien keer zoveel waard als de plek rechts ervan.
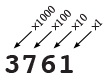
In het binaire talstelsel, zijn er maar 2 cijfers (0 en 1) en is iedere plek twee
keer zoveel waard als de plek rechts ervan.
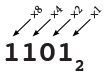
-
 Kijk even hoe dit Snap!-progamma wordt uitgevoerd.
Beschrijf het gedrag van de binaire teller. Leg uit wat je ziet.
Kijk even hoe dit Snap!-progamma wordt uitgevoerd.
Beschrijf het gedrag van de binaire teller. Leg uit wat je ziet.
Binaire Notatie Lezen
In het decimale talstelsel, staat iedere plek voor een macht van tien: De plek van de eenheden (100 = 1), de plek van de tientallen (101 = 10), de plek van de honderdtallen (102 = 100), de plek van de duizendtallen (103 = 1000), etc. Dus, bijvoorbeeld:
9827 = 9 × 103 + 8 × 102 + 2 × 101 + 7 × 100
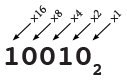 Het binaire talstelsel werkt hetzelfde maar met machten van twee in
plaats van machten van tien. De plekken gaan zo: De plek van de eenheden (20 = 1), de plek
van de tweetallen(21 = 2), de plek van de viertallen (22 = 4), de plek van de
achttallen (23 = 8), de plek van de zestientallen (24 = 16), etc. Dus,
bijvoorbeeld:
Het binaire talstelsel werkt hetzelfde maar met machten van twee in
plaats van machten van tien. De plekken gaan zo: De plek van de eenheden (20 = 1), de plek
van de tweetallen(21 = 2), de plek van de viertallen (22 = 4), de plek van de
achttallen (23 = 8), de plek van de zestientallen (24 = 16), etc. Dus,
bijvoorbeeld:
100102 = 1 × 24 + 0 × 23 + 0 × 22 + 1 × 21 + 0 × 20 = 16 + 2 = 1810
Om te vertalen van binair naar het decimale talstelsel schrijven we eerst het getal op papier. Daarna schrijven we de waardes van iedere plek door de waarde van de rechterpositie te verdubbelen:
| 1 | 0 | 1 | 1 | 0 | 1 |
|---|---|---|---|---|---|
| 32 | 16 | 8 | 4 | 2 | 1 |
 |
|||||
Dit betekent dat het getal, in het decimale talstelsel 1 + 4 + 8 + 32 = 45 is. Dus, 1011012 = 4510.
- Vertaal deze binaire getallen naar het decimale talstelsel:
- 1012
- 1112
- 10100112
- 10000000002
Schrijven in binaire notatie
Om te vertalen van het decimale talstelsel naar binair, schrijven we eerst de waardes van de binaire plekken van rechts naar links op door de waarde van de rechterpositie te verdubbelen, dus 1, 2, 4, 8 enzovoort. Dit doe je totdat je een waarde krijgt die groter is dan het getal dat je wil gaan opschrijven in binair. Als voorbeeld gaan we het getal 89 omschrijven naar binair, als je deze stap goed gevolgd hebt dan heb je nu een tabel zoals hieronder.
 |
|||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
Bedenk nu "ik kan 64 van 89 aftrekken, dus ik schrijf een 1 daaronder en dan blijft er 25 over (89-64). Ik schrijf nu een 0 bij 32 omdat ik niet 32 van 25 af kan trekken omdat 32 groter dan 25 is. Ik kan wel 16 eraf halen en dan blijft er 9 over, dus de bit voor 16 wordt ook 1. Als we dit proces blijven herhalen dan zien we dat de bits ook 1 worden voor 8 en 1 (25-16 = 9, 9 - 8 = 1, 1-1 = 0). "
| 0 |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 0 | 1 |
Lees nu het getal af: 10110012 = 8910.
Hieronder staat een meer precieze beschrijving van dit algoritme om de binaire representatie van elk positief heel getal te vinden:
- Vind de grootste macht van twee die kleiner is dan het getal dat je om wil schrijven naar binair.
- Trek daarna die macht af van het getal en schrijf een 1 op. Onthoud het nieuwe getal.
- Vind dan de op-één-na-grootste macht van 2 voor het originele getal en:
- Als het kleiner is dan het nieuwe getal, trek het af van het nieuwe getal, onthoud het nieuwe getal en schrijf weer een 1 op.
- Als het groter is dan het nieuwe getal, schrijf dan een nul op.
De rij enen en nullen die je overhoudt is de binaire versie van je originele getal.
- Schrijf deze getallen in het decimale talstelsel om naar binair:
- 63
- 64
- 65
- 129
- 128
- 127